For the past several years, I've been using Advent of Code as an excuse to do some professional development and learn new languages. The past two years, I used Rust, which is an interesting language.
I remembered seeing funny looking solutions on the Reddit AOC solutions thread that were basically a jumble of symbols. These were for a language called Uiua, which naturally piqued my interest.
For some reason, I decided to try to do AOC 2024 in Uiua. It has not been a smooth ride, and in this blog post I'll briefly touch on some of my thoughts and experiences in Uiua and two other array programming langauges, APL and BQN.
Starting in Uiua
The Uiua website describes the language as:
Uiua (wee-wuh 🔉) is a general purpose, stack-based, array-oriented programming language with a focus on simplicity, beauty, and tacit code.
Uiua lets you write code that is as short as possible while remaining readable, so you can focus on problems rather than ceremony.
The language is not yet stable, as its design space is still being explored. However, it is already quite powerful and fun to use!
But this screenshot of a basic Uiua example probably gives you a better idea how the language works:
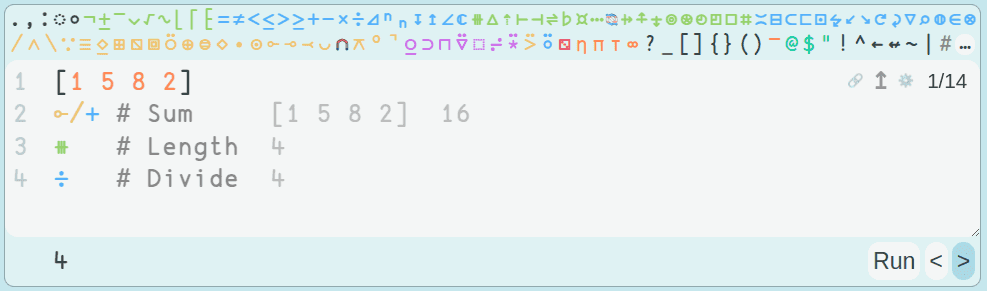
I spent a while going through the Uiua tutorials, and I made it through the first few AOC problems with a bit of difficulty.
I eventually got to a problem where I had to write a fold. And I remember getting extremely frustrated with the language. The language does not have (local) variable names. Instead, everything is on the stack. You as the programmer must internally keep track of the stack and how all the operations you perform modify it. Oh, it's a stack-based machine too, so the top of the stack is constantly changing.
I think there were only three or four values I had to juggle in my fold function, but it was too much. Maybe because I work in binary analysis where you can't take local variables for granted, I really want to be able to use them in my "high level" programming languages.
More seriously, I think the lack of local variables just compounds complexity. Simple functions are fine. But complex functions, which are already complex, start to get even more complex as the programmer now has to deal with juggling the stack layout. No thanks.
Moving to APL
Uiua is an array-oriented programming language. Most array-oriented programming languages derive from APL (which was created in the 60s!) One of the benefits of this is that it's a pretty mature language, and there is a lot of training material available for it.
The most popular implementation is a commercial, non-open-source one called Dyalog APL. I wasn't thrilled to be using a closed-source implementation, but it's just for learning purposes so I supposed it was fine. I started following along with this tutorial. I got about half way through, and started to feel like I was probably competent enough to try some AOC problems in APL.
I immediately ran into trouble again, but this time with APL's tooling. I have two basic requirements for a programming language for AoC:
- I can put the code for each day in a file.
- I can run the code from inside VS code fairly easily.
- I can type the weird symbols of the language from within VS code. (Oops, this one is new this year.)
I forgot to mention that Uiua's tooling was pretty great. No complaints; I installed the extension and everything worked as expected.
APL tooling is weird. It's not really designed like modern programming languages. Instead, all coding is supposed to be done in workspaces. I was pretty frustrated by this and I eventually gave up.
In retrospect, I may have been able to get by with dyalogscript. But the
unpolished nature of the tooling, at least for how programming languages are
used in this century, was a big turn off.
BQN
Finally, I landed on BQN. Here is the website's description:
Looking for a modern, powerful language centered on Ken Iverson's array programming paradigm? BQN now provides:
- A simple, consistent, and stable array programming language
- A low-dependency C implementation using bytecode compilation: installation
- System functions for math, files, and I/O (including a C FFI)
- Documentation with examples, visuals, explanations, and rationale for features
- Libraries with interfaces for common file formats like JSON and CSV
And here's a quick example from the website.
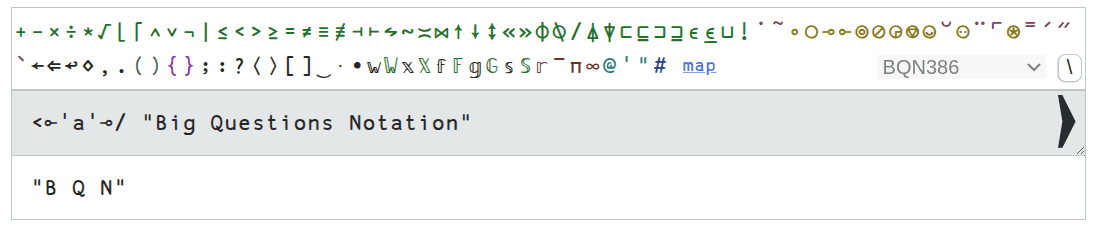
If you are thinking that all of these languages look pretty similar, you're right.
BQN had a lot going for it. It wasn't stack based. The tooling seemed pretty good. Not only is the language designed to be used from files, you can even use multiple files. Welcome to the 21st century baby!
I also liked the name. The whole point of learning this array-programming paradigm was to be able to write short, concise code. So the idea of answering "Big Questions" was appealing.
BQN has a lot of documentation. There are a few tutorials intended for new users, but most of the documentation is of the, well, documentation variety. It's not a tutorial, but a reference manual. It's written by an absolute array programming expert, for other array programming experts. It's not the most beginner friendly.
So it was a pretty rough learning curve. I quickly joined the APL language discord and started asking a lot of questions. People there are very patient and helpful, thankfully! I also found some other people working on AOC, and I spent a lot of time unraveling their solutions.
I just finished Day 9 of AOC 2024 in BQN. It's December 20th, so obviously I'm pretty far behind. I'm not sure if I'll finish this year; I've been trying to embrace learning the array-oriented way of thinking, which has been challenging and slow.
Readability
I've been slowly getting better at reading others' BQN code, but it's hard. There are a lot of symbols to remember, but that's really not the main problem for me. Instead, it's very difficult to "parse" where parentheses should be placed. It can also be difficult to follow the general flow of very terse code.
Here's a snippet of code from RubenVerg who is a genius when it comes to tacit coding in BQN.
in←•file.Chars "input/8.txt"
P←(¬-˜⊢×·+`»⊸>)⊸⊔
OutOfBounds←∨´(0>⊢)∾≢⊸≤
Parse←>' '⊸<⊸P
Part1←{𝕊grid: ≠¬∘(grid⊸OutOfBounds)¨⊸/⍷∾⥊{(𝕨(≢∧=○(⊑⟜grid)∧'.'≠grid⊑˜⊢)𝕩)/⋈𝕩-˜2×𝕨}⌜˜⥊↕≢ grid}Parse(Holy smokes, my formatter actually supports BQN!)
Part1 is a function that is composed with Parse. So it will Parse the input and the result will be bound to grid inside the curly brackets.
I have my doubts that anyone can read this code. Rather, you can reverse engineer it by breaking it down into smaller pieces and understanding each piece. But it's not easy to read, even if you understand what all the symbols mean.
Tacit coding
According to the BQN documentation:
Tacit programming (or "point-free" in some other languages) is a term for defining functions without referring to arguments directly, which in BQN means programming without blocks.
The idea of tacit coding is kind of cool. You basically avoid applying functions and instead compose and otherwise modify them.
BQN has a function composition operator ∘ just like you would imagine. But a lot of tacit code uses trains. For a pretty poor introduction to trains, you can view this page. But let me spell out the basics.
A 2-train is two adjacent functions, and by definition fg evaluates to f∘g
(f composed with g). In other words, to evaluate fg on an input 𝕩, we
could use g(f(𝕩)). (A BQN programmer would never write that and would
instead just use g f 𝕩.)
3-trains, which consist of three adjacent functions, are where things get fun.
Again, by definition, evaluating fgh on input 𝕩 evaluates to (f 𝕩) g (h 𝕩). This is not very intuitive, but it's useful for a couple reasons:
𝕩appears twice, so you can use it to avoid writing a long expression multiple times- There's a fork, so you can combine two different behaviors
gacts as a summarizer or combiner
Here's an example I used in my solution to Day 9:
(⊣×(↕≠)) argThe 3-train consists of ⊣, ×, and (↕≠). In my program, arg is actually an
extremely long expression, and I did not want to write it twice. Let's expand
the train:
(⊣ arg) × (↕≠ arg)⊣ is the identity function, so it returns arg. × is multiplication. ≠
returns the length of its (right) argument, and ↕ returns the list of numbers
from 0 to one less than its argument. So this train multiplies each element in
arg (it's an array) by its index. Pretty cool, huh?
The trouble is that when reading and writing BQN code, it can be difficult to
identify trains. I've been getting better, but I still find myself inserting a
∘ whenever my code doesn't work, since function composition will "stop" a
train from forming when it wasn't intentional. Now look at RubenVerg's code
above and think about all the trains. Even if you understand the symbols, it's
not easy. This is very much a learned skill!
Here's a very basic example of how parsing influences trains. BQN evaluates
from right to left. So if you write fgh 𝕩, that actually means f(g(h(𝕩)))
and there is not a train. But (fgh) 𝕩 is completely different and fgh is a
3-train. Now again, look at RubenVerg's code and try to figure out the implied
parentheses. Good luck!
Documentation
I found BQN's documentation to be very thorough, but not very beginner friendly. I think it's written by an expert for other experts. In some cases, it seems to pontificate and misses basic definitions. For example, the trains page doesn't directly define 2- and 3-trains. You can probably figure out the definition from the examples, but it's not ideal.
On the plus side, many documentation pages feature very intuitive diagrams. See the below diagram in Group for an example.
Cool features
There are some cool features in BQN. I'm not going to cover all of them, but here are ones that stand out based on my programming career.
Group ⊔
The Group ⊔ operator is pretty nifty. Here is a nice diagram that intuitively
depicts an example.
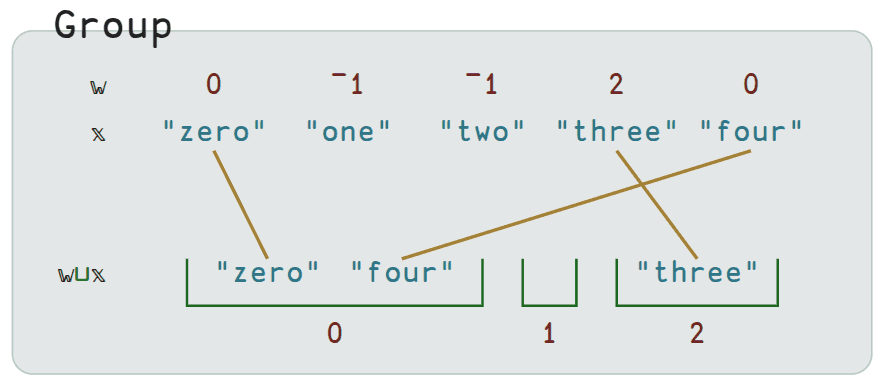
In BQN, 𝕨 is the left argument and 𝕩 is the right argument. Usually 𝕩
is some existing structure you want to analyze, and 𝕨 is a list of indices
that you construct to define the groupings you want. If you want elements to be
placed in the same group, you assign them the same index.
This is a powerful capability. For example, in today's AOC problem, there was a string like 00...111...2...333.44.5555.6666.777.888899 where group 0 had size two, group 1 had size 3, and so on. One easy way to determine the size of each group in BQN is using Group ⊔. If you first change each . to a -1, you can use the same array as both arguments with ⊔˜ to get the groupings, and ≠¨⊔˜ to get the length of each grouping. (≠ means length and ¨ means to modify the function to the left to apply to each element of the array to the right.)
Under ⌾
Under ⌾ is an interesting capability that is a bit tricky to explain. Here is
the official explanation from the
documentation:
The Under 2-modifier expresses the idea of modifying part of an array, or applying a function in a different domain, such as working in logarithmic space. It works with a transformation 𝔾 that applies to the original argument 𝕩, and a function 𝔽 that applies to the result of 𝔾 (and if 𝕨 is given, 𝔾𝕨 is used as the left argument to 𝔽). Under does the "same thing" as 𝔽, but to the original argument, by applying 𝔾, then 𝔽, then undoing 𝔾 somehow.
So to restate, there is a transformation or selection operation, 𝔾, and a
modification transformation 𝔽. There are different applications, but I
always used this to transform or change part of an array. In that case, 𝔾 might be a filter, and 𝔽 describes how you want to change the array.
Here's an example from today's AOC again:
ReplaceNegWithNegOne ← {¯1¨⌾((𝕩<0)⊸/) 𝕩}I'm not going to try to explain all the syntax. But 𝔾 is ((𝕩<0)⊸/); this
says to filter 𝕩 so that only elements less than 0 remain. 𝔽 is ¯1¨,
which means return negative one for each argument. So, put together, replace
negative elements with negative one. I then used the resulting array as an
index to Group ⊔, which ignores any element with an index of negative one.
This is kind of neat because values are immutable in BQN, and this provides an efficient way to change part of them. I assume that the implementation uses this to avoid making copies of the whole array.
Not So Cool Features
One thing that annoys me about BQN is that a number of basic functions are not built-in because they can be succinctly expressed.
For example, want to split a string? You'd better memorize
x0((⊢-˜+`׬)∘=⊔⊢)y1 #Split y1 at occurrences of separators x0, removing the separatorsWant to build a number from an array of digits? You can use
10⊸×⊸+˜´⌽d1 # Natural number from base-10 digitsThese both come from BQNcrate, a
repository of useful functions you could but probably don't want to derive
yourself. I'd much rather see this in a standard library of some sort. Most of
these are cool, and it's fun to see how they work. But when I'm actually
coding, I don't want to look these up or try to derive them. I just want to say
split the string by ' ' and move on.
I don't think I'm alone. I've noticed that RubenVerg for example likes to use
•ParseFloat to parse integers rather than
(10⊸×⊸+˜´∘⌽-⟜'0')d1 #Parse natural number from stringwhich doesn't exactly roll off the tongue.
Ed's Feelings on BQN
Unfortunately, I don't have fun programming in BQN. There, I said it. I've literally felt very stupid at times trying to figure out how to write a simple function.
BQN is challenging, and I like challenges. But it's a fine line. There is an intense gratification to stringing together a whole bunch of opaque symbols that very few other people can read. But it's also frustrating and demoralizing to spend hours trying to figure out how to solve a basic problem.
It's hard to say how much of this is just part of learning a new paradigm. I remember when I first learned OCaml as a graduate student and had to figure out how to think functionally and decode arcane type errors involving parametric polymorphism. At the time, it was hard (and probably not that fun, but I can't remember). Now it's second nature. Maybe BQN will become second nature if I stick with it.
Conclusion
I probably won't be using BQN for any real projects any time soon. But I haven't given up on it entirely. I may try to finish AOC 2024 in BQN. We'll see. Given the lack of fun I've been having, I can't say I'm extremely motivated to do so. So for now I'll be taking things one day at a time.
If you're curious about my BQN code, you can find my AOC 2024 solutions here.
Powered with by Gatsby 5.0