For the past several years, I've been using Advent of Code as an excuse to do some professional development and learn new languages. The past two years, I used Rust, which is an interesting language.

I remembered seeing funny looking solutions on the Reddit AOC solutions thread that were basically a jumble of symbols. These were for a language called Uiua, which naturally piqued my interest.

For some reason, I decided to try to do AOC 2024 in Uiua. It has not been a smooth ride, and in this blog post I'll briefly touch on some of my thoughts and experiences in Uiua and two other array programming langauges, APL and BQN.

Starting in Uiua

The Uiua website describes the language as:

Uiua (wee-wuh 🔉) is a general purpose, stack-based, array-oriented programming language with a focus on simplicity, beauty, and tacit code.

Uiua lets you write code that is as short as possible while remaining readable, so you can focus on problems rather than ceremony.

The language is not yet stable, as its design space is still being explored. However, it is already quite powerful and fun to use!

But this screenshot of a basic Uiua example probably gives you a better idea how the language works:

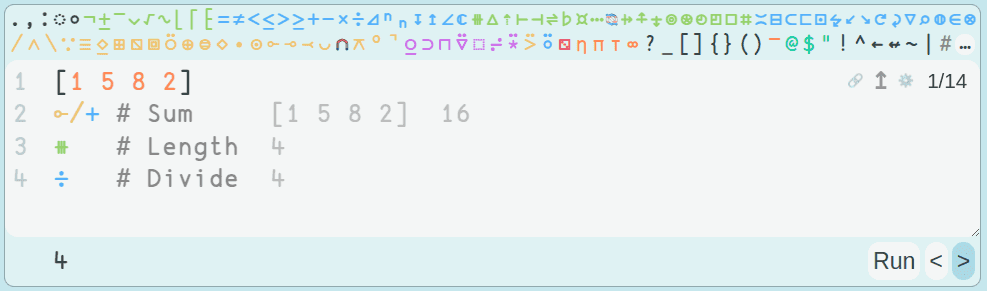
I spent a while going through the Uiua tutorials, and I made it through the first few AOC problems with a bit of difficulty.

I eventually got to a problem where I had to write a fold. And I remember getting extremely frustrated with the language. The language does not have (local) variable names. Instead, everything is on the stack. You as the programmer must internally keep track of the stack and how all the operations you perform modify it. Oh, it's a stack-based machine too, so the top of the stack is constantly changing.

I think there were only three or four values I had to juggle in my fold function, but it was too much. Maybe because I work in binary analysis where you can't take local variables for granted, I really want to be able to use them in my "high level" programming languages.

More seriously, I think the lack of local variables just compounds complexity. Simple functions are fine. But complex functions, which are already complex, start to get even more complex as the programmer now has to deal with juggling the stack layout. No thanks.

Moving to APL

Uiua is an array-oriented programming language. Most array-oriented programming languages derive from APL (which was created in the 60s!) One of the benefits of this is that it's a pretty mature language, and there is a lot of training material available for it.

The most popular implementation is a commercial, non-open-source one called Dyalog APL. I wasn't thrilled to be using a closed-source implementation, but it's just for learning purposes so I supposed it was fine. I started following along with this tutorial. I got about half way through, and started to feel like I was probably competent enough to try some AOC problems in APL.

I immediately ran into trouble again, but this time with APL's tooling. I have two basic requirements for a programming language for AoC:

1. I can put the code for each day in a file.
2. I can run the code from inside VS code fairly easily.
3. I can type the weird symbols of the language from within VS code. (Oops, this one is new this year.)

I forgot to mention that Uiua's tooling was pretty great. No complaints; I installed the extension and everything worked as expected.

APL tooling is weird. It's not really designed like modern programming languages. Instead, all coding is supposed to be done in workspaces. I was pretty frustrated by this and I eventually gave up.

In retrospect, I may have been able to get by with dyalogscript. But the unpolished nature of the tooling, at least for how programming languages are used in this century, was a big turn off.

BQN

Finally, I landed on BQN. Here is the website's description:

Looking for a modern, powerful language centered on Ken Iverson's array programming paradigm? BQN now provides:

• A simple, consistent, and stable array programming language
• A low-dependency C implementation using bytecode compilation: installation
• System functions for math, files, and I/O (including a C FFI)
• Documentation with examples, visuals, explanations, and rationale for features
• Libraries with interfaces for common file formats like JSON and CSV

And here's a quick example from the website.

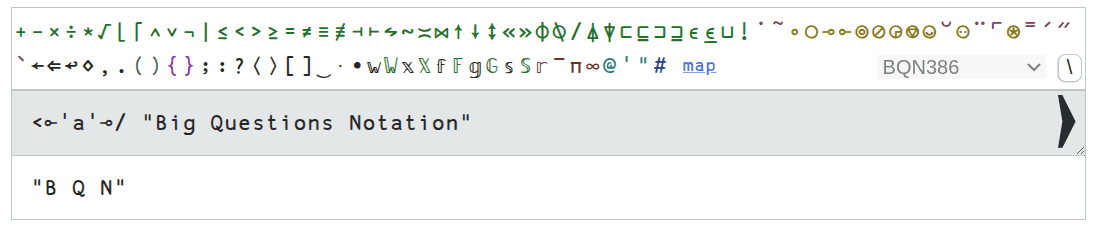
If you are thinking that all of these languages look pretty similar, you're right.

BQN had a lot going for it. It wasn't stack based. The tooling seemed pretty good. Not only is the language designed to be used from files, you can even use multiple files. Welcome to the 21st century baby!

I also liked the name. The whole point of learning this array-programming paradigm was to be able to write short, concise code. So the idea of answering "Big Questions" was appealing.

BQN has a lot of documentation. There are a few tutorials intended for new users, but most of the documentation is of the, well, documentation variety. It's not a tutorial, but a reference manual. It's written by an absolute array programming expert, for other array programming experts. It's not the most beginner friendly.

So it was a pretty rough learning curve. I quickly joined the APL language discord and started asking a lot of questions. People there are very patient and helpful, thankfully! I also found some other people working on AOC, and I spent a lot of time unraveling their solutions.

I just finished Day 9 of AOC 2024 in BQN. It's December 20th, so obviously I'm pretty far behind. I'm not sure if I'll finish this year; I've been trying to embrace learning the array-oriented way of thinking, which has been challenging and slow.

Readability

I've been slowly getting better at reading others' BQN code, but it's hard. There are a lot of symbols to remember, but that's really not the main problem for me. Instead, it's very difficult to "parse" where parentheses should be placed. It can also be difficult to follow the general flow of very terse code.

Here's a snippet of code from RubenVerg who is a genius when it comes to tacit coding in BQN.

in←•file.Chars "input/8.txt"

P←(¬-˜⊢×·+`»⊸>)⊸⊔
OutOfBounds←∨´(0>⊢)∾≢⊸≤

Parse←>' '⊸<⊸P

Part1←{𝕊grid: ≠¬∘(grid⊸OutOfBounds)¨⊸/⍷∾⥊{(𝕨(≢∧=○(⊑⟜grid)∧'.'≠grid⊑˜⊢)𝕩)/⋈𝕩-˜2×𝕨}⌜˜⥊↕≢ grid}Parse

(Holy smokes, my formatter actually supports BQN!)

Part1 is a function that is composed with Parse. So it will Parse the input and the result will be bound to grid inside the curly brackets.

I have my doubts that anyone can read this code. Rather, you can reverse engineer it by breaking it down into smaller pieces and understanding each piece. But it's not easy to read, even if you understand what all the symbols mean.

Tacit coding

According to the BQN documentation:

Tacit programming (or "point-free" in some other languages) is a term for defining functions without referring to arguments directly, which in BQN means programming without blocks.

The idea of tacit coding is kind of cool. You basically avoid applying functions and instead compose and otherwise modify them.

BQN has a function composition operator ∘ just like you would imagine. But a lot of tacit code uses trains. For a pretty poor introduction to trains, you can view this page. But let me spell out the basics.

A 2-train is two adjacent functions, and by definition fg evaluates to f∘g (f composed with g). In other words, to evaluate fg on an input 𝕩, we could use g(f(𝕩)). (A BQN programmer would never write that and would instead just use g f 𝕩.)

3-trains, which consist of three adjacent functions, are where things get fun. Again, by definition, evaluating fgh on input 𝕩 evaluates to (f 𝕩) g (h 𝕩). This is not very intuitive, but it's useful for a couple reasons:

• 𝕩 appears twice, so you can use it to avoid writing a long expression multiple times
• There's a fork, so you can combine two different behaviors
• g acts as a summarizer or combiner

Here's an example I used in my solution to Day 9:

(⊣×(↕≠)) arg

The 3-train consists of ⊣, ×, and (↕≠). In my program, arg is actually an extremely long expression, and I did not want to write it twice. Let's expand the train:

(⊣ arg) × (↕≠ arg)

⊣ is the identity function, so it returns arg. × is multiplication. ≠ returns the length of its (right) argument, and ↕ returns the list of numbers from 0 to one less than its argument. So this train multiplies each element in arg (it's an array) by its index. Pretty cool, huh?

The trouble is that when reading and writing BQN code, it can be difficult to identify trains. I've been getting better, but I still find myself inserting a ∘ whenever my code doesn't work, since function composition will "stop" a train from forming when it wasn't intentional. Now look at RubenVerg's code above and think about all the trains. Even if you understand the symbols, it's not easy. This is very much a learned skill!

Here's a very basic example of how parsing influences trains. BQN evaluates from right to left. So if you write fgh 𝕩, that actually means f(g(h(𝕩))) and there is not a train. But (fgh) 𝕩 is completely different and fgh is a 3-train. Now again, look at RubenVerg's code and try to figure out the implied parentheses. Good luck!

Documentation

I found BQN's documentation to be very thorough, but not very beginner friendly. I think it's written by an expert for other experts. In some cases, it seems to pontificate and misses basic definitions. For example, the trains page doesn't directly define 2- and 3-trains. You can probably figure out the definition from the examples, but it's not ideal.

On the plus side, many documentation pages feature very intuitive diagrams. See the below diagram in Group for an example.

Cool features

There are some cool features in BQN. I'm not going to cover all of them, but here are ones that stand out based on my programming career.

Group ⊔

The Group ⊔ operator is pretty nifty. Here is a nice diagram that intuitively depicts an example.

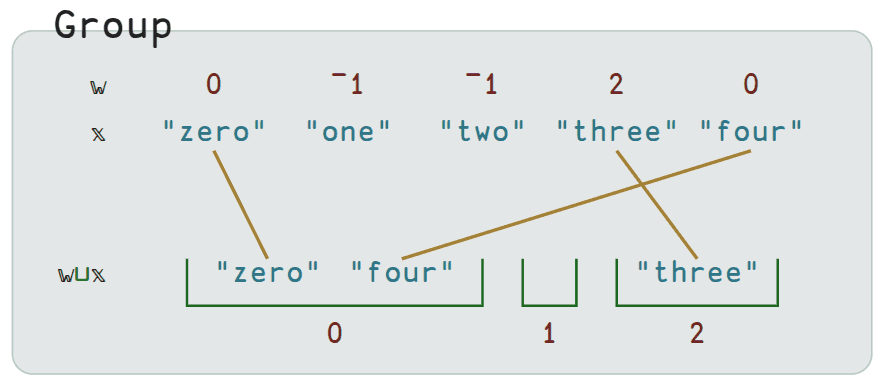
In BQN, 𝕨 is the left argument and 𝕩 is the right argument. Usually 𝕩 is some existing structure you want to analyze, and 𝕨 is a list of indices that you construct to define the groupings you want. If you want elements to be placed in the same group, you assign them the same index.

This is a powerful capability. For example, in today's AOC problem, there was a string like 00...111...2...333.44.5555.6666.777.888899 where group 0 had size two, group 1 had size 3, and so on. One easy way to determine the size of each group in BQN is using Group ⊔. If you first change each . to a -1, you can use the same array as both arguments with ⊔˜ to get the groupings, and ≠¨⊔˜ to get the length of each grouping. (≠ means length and ¨ means to modify the function to the left to apply to each element of the array to the right.)

Under ⌾

Under ⌾ is an interesting capability that is a bit tricky to explain. Here is the official explanation from the documentation:

The Under 2-modifier expresses the idea of modifying part of an array, or applying a function in a different domain, such as working in logarithmic space. It works with a transformation 𝔾 that applies to the original argument 𝕩, and a function 𝔽 that applies to the result of 𝔾 (and if 𝕨 is given, 𝔾𝕨 is used as the left argument to 𝔽). Under does the "same thing" as 𝔽, but to the original argument, by applying 𝔾, then 𝔽, then undoing 𝔾 somehow.

So to restate, there is a transformation or selection operation, 𝔾, and a modification transformation 𝔽. There are different applications, but I always used this to transform or change part of an array. In that case, 𝔾 might be a filter, and 𝔽 describes how you want to change the array.

Here's an example from today's AOC again:

ReplaceNegWithNegOne ← {¯1¨⌾((𝕩<0)⊸/) 𝕩}

I'm not going to try to explain all the syntax. But 𝔾 is ((𝕩<0)⊸/); this says to filter 𝕩 so that only elements less than 0 remain. 𝔽 is ¯1¨, which means return negative one for each argument. So, put together, replace negative elements with negative one. I then used the resulting array as an index to Group ⊔, which ignores any element with an index of negative one.

This is kind of neat because values are immutable in BQN, and this provides an efficient way to change part of them. I assume that the implementation uses this to avoid making copies of the whole array.

Not So Cool Features

One thing that annoys me about BQN is that a number of basic functions are not built-in because they can be succinctly expressed.

For example, want to split a string? You'd better memorize

x0((⊢-˜+`׬)∘=⊔⊢)y1 #Split y1 at occurrences of separators x0, removing the separators

Want to build a number from an array of digits? You can use

10⊸×⊸+˜´⌽d1 # Natural number from base-10 digits

These both come from BQNcrate, a repository of useful functions you could but probably don't want to derive yourself. I'd much rather see this in a standard library of some sort. Most of these are cool, and it's fun to see how they work. But when I'm actually coding, I don't want to look these up or try to derive them. I just want to say split the string by ' ' and move on.

I don't think I'm alone. I've noticed that RubenVerg for example likes to use •ParseFloat to parse integers rather than

(10⊸×⊸+˜´∘⌽-⟜'0')d1 #Parse natural number from string

which doesn't exactly roll off the tongue.

Ed's Feelings on BQN

Unfortunately, I don't have fun programming in BQN. There, I said it. I've literally felt very stupid at times trying to figure out how to write a simple function.

BQN is challenging, and I like challenges. But it's a fine line. There is an intense gratification to stringing together a whole bunch of opaque symbols that very few other people can read. But it's also frustrating and demoralizing to spend hours trying to figure out how to solve a basic problem.

It's hard to say how much of this is just part of learning a new paradigm. I remember when I first learned OCaml as a graduate student and had to figure out how to think functionally and decode arcane type errors involving parametric polymorphism. At the time, it was hard (and probably not that fun, but I can't remember). Now it's second nature. Maybe BQN will become second nature if I stick with it.

Conclusion

I probably won't be using BQN for any real projects any time soon. But I haven't given up on it entirely. I may try to finish AOC 2024 in BQN. We'll see. Given the lack of fun I've been having, I can't say I'm extremely motivated to do so. So for now I'll be taking things one day at a time.

If you're curious about my BQN code, you can find my AOC 2024 solutions here.

Hello, Merry Christmas and Happy Holidays! I just completed Advent of Code 2023, and wanted to jot down a few reflections before I disappear for the holidays. Like last year, I chose to implement my solutions using Rust.

Rust: easier with practice, but still a bit in the way

The good news is that I ran into far fewer problems with Rust this year. There are a few reasons for this, but a lot of it just boils down to experience. I tend to program excessively using lazy iterators, and I began to get a second sense for when I'd need to call .collect() to avoid referencing a freed temporary value. Similarly, when I would get a compiler error (and yes, this still happens a lot!), I would often immediately know how to fix the problem.

That being said, there were still occasions when the language just "got in the way". I had a few solutions where I had to throw in copious amounts of .clone() calls. One salient example was on day 22 when I wanted to memoize a subproblem. But to do so, I also had to pass a value instead of a reference to each sub-problem, which slowed things down dramatically. Anyway, with more work, the solution probably would have been to use references with lifetimes and just ensure that memoization happened during the right lifetimes. But the key phrase there is with more work. And see below -- I was already pretty frustrated.

Chat-GPT and Co-pilot

On this year's Advent of Code, I used Chat-GPT and Co-pilot quite heavily, as I do in practice when coding. I used Chat-GPT mostly to avoid looking up documentation or crates. For example, "How can I add a progress indicator to an iterator in Rust?" or "How can I bind a sub-pattern to a name in Rust?". Given that I hadn't programmed in Rust for a year, I was a bit rusty (ha!)

Co-pilot was also quite useful. It was pretty good at writing out boilerplate code. Advent of Code problems tend to include copious amounts of grid problems, and Co-pilot reduced a lot of the fatigue for helper functions. Define things for the X axis, and it would figure out how to implement the other cases.

I also found that Co-pilot was able to explain weird Rust borrowing problems far better than the compiler. As I wrote about last year, Rust's borrowing rules sometimes don't work that great for my programming style, but Co-pilot was pretty good about explaining problems. I don't have a specific example, but think of searching a vector using vec.iter(), using the found value at some point, and then later trying to move the vector. In my opinion, this definitely makes it easier to program in Rust.

Now, Co-pilot did introduce some headaches as well. Although it was pretty good, it would sometimes introduce problematic completions. For instance, it really liked to complete print statements by adding an extra quote, e.g., println!("This is something: {:?}", something"); Not a huge deal, but it happened enough that it was irritating.

Frustration and Clear-headedness: The Fine Line Between Perseverance and Stubbornness

On some level, I think everyone knows this, but it's still worth saying: You are more effective when thinking clearly. I recall from graduate school that many of my fellow students would pull all nighters and submit papers in the wee hours of the morning. I never did that. My efficiency just plummets as I get tired.

I experienced a pretty funny (in retrospect) example of this on day 22. You can read the problem, it's not really that hard. One of the nice things about programming functionally is that it usually works or completely fails. There's not a lot of in-between. In Advent of Code, this means that if your solution works on the example, it usually works on the real input (ignoring performance). But on day 22, my code did not work on the real input. The problem is pretty simple, so it was infuriating. Rather than taking a break to clear my head, I just kept trying to debug it. I stayed up far past my bed time, becoming more and more frustrated. I even completely rewrote my implementation in Python before giving up and going to bed.

The next morning, I woke up and looked at the problem again. I had a simple idea. I actually had two solutions to the problem. I had a simple but slow solution that I was confident was correct, but was too slow to use on the real input. And I had my fast solution that I thought should be correct, but wasn't. My insight was that I could make "in between" problems by just taking a portion of the real input -- say 10%. And then see if my fast solution agreed with the slow one. It didn't. I then ran Lithium and reduced the input to a minimal example. From here, it was trivial to spot the fundamental problem I had in my recursive algorithm. I fixed it, and my solution worked. This whole process probably only took 30 minutes from the time I woke up. I futilely spent hours the previous night. And the worst part is that, even in the moment, I knew I was acting foolishly. I was just too frustrated to stop.

I don't know if this is universal, but when I am stressed or frustrated, I usually make mistakes, which naturally compound my stress and frustration! There is a fine line between perseverance and stubbornness, and I crossed it on day 22.

I've been working on a blog post that has some interesting images in it. Unfortunately, my blog view is narrow, which makes it hard to see these. So, I decided to add a "click for full screen" feature to my blog. How hard could it be?

Answer: Very hard. Sadly, this took me a few days.

I hope to write a more detailed post about this later, but for now, I wanted to show off the fruits of my labor.

I can write:

<fsclick>![A wide picture](wide.jpg)</fsclick>

And you see:

Go ahead, click on it, I dare you! src

Last December, I did most of Advent of Code in Rust, which I had never used before. You can find my solutions here.

The Good

Modern syntax with LLVM codegen

I tend to program functionally, perhaps even excessively so. I try to express most concepts through map, filter, and fold. I tend to enjoy languages that make this easy. Fortunately, this is becoming the norm, even in non-functional languages such as Python, Java and C++.

Perhaps it is not too surprising then that Rust, as a new language, supports this style of programming as well:

let x: i32 = (1..42).map(|x| x+1).sum();
println!("x: {x}");

What is truly amazing about Rust though is how this function code is compiled to x86-64. At optimiation level 1, the computation of x evaluates to

        mov     dword ptr [rsp + 4], 902
        lea     rax, [rsp + 4]

Yes, the compiler is able to unfold and simplify the entire computation, which is pretty neat. But let's look at the code at optimization level 0:

        mov     ecx, 1
        xor     eax, eax
        mov     dl, 1
.LBB5_1:
.Ltmp27:
        movzx   edx, dl
        and     edx, 1
        add     edx, ecx
.Ltmp28:
        add     eax, ecx
        inc     eax
        mov     ecx, edx
.Ltmp29:
        cmp     edx, 42
        setb    dl
.Ltmp30:
        jb      .LBB5_1
.Ltmp31:
        sub     rsp, 72
        mov     dword ptr [rsp + 4], eax
        lea     rax, [rsp + 4]

So our functional computation of a range, a map, and a sum (which is a reduce) is compiled into a pretty simple loop. And keep in mind this is at optimization level 0.

By contrast, let's take a look at how OCaml handles this. First, the included OCaml standard library is not so great, so writing the program is more awkward:

let r = List.init 42 (fun x -> x + 1) in
let x = List.map (fun x -> x+1) r in
let x = List.fold_left (+) 0 x in
Printf.printf "x: %x\n" x

But let's look at the assembly with aggressive optimizations:

camlExample__entry:
        leaq    -328(%rsp), %r10
        cmpq    32(%r14), %r10
        jb      .L122
.L123:
        subq    $8, %rsp
.L121:
        movl    $85, %ebx
        movl    $5, %eax
        call    camlExample__init_aux_432@PLT
.L124:
        call    caml_alloc2@PLT
.L125:
        leaq    8(%r15), %rsi
        movq    $2048, -8(%rsi)
        movq    $5, (%rsi)
        movq    %rax, 8(%rsi)
        movq    camlExample__Pmakeblock_arg_247@GOTPCREL(%rip), %rdi
        movq    %rsp, %rbp
        movq    56(%r14), %rsp
        call    caml_initialize@PLT
        movq    %rbp, %rsp
        movq    camlExample__Pmakeblock_arg_247@GOTPCREL(%rip), %rax
        movq    (%rax), %rax
        call    camlExample__map_503@PLT
.L126:
        call    caml_alloc2@PLT
.L127:
        leaq    8(%r15), %rsi
        movq    $2048, -8(%rsi)
        movq    $5, (%rsi)
        movq    %rax, 8(%rsi)
        movq    camlExample__x_77@GOTPCREL(%rip), %rdi
        movq    %rsp, %rbp
        movq    56(%r14), %rsp
        call    caml_initialize@PLT
        movq    %rbp, %rsp
        movq    camlExample__x_77@GOTPCREL(%rip), %rax
        movq    (%rax), %rax
        movq    8(%rax), %rbx
        movl    $5, %eax
        call    camlExample__fold_left_558@PLT
.L128:
        movq    camlExample__x_75@GOTPCREL(%rip), %rdi
        movq    %rax, %rsi
        movq    %rsp, %rbp
        movq    56(%r14), %rsp
        call    caml_initialize@PLT
        movq    %rbp, %rsp
        movq    camlExample__const_block_49@GOTPCREL(%rip), %rdi
        movq    camlExample__Pmakeblock_637@GOTPCREL(%rip), %rbx
        movq    camlStdlib__Printf__anon_fn$5bprintf$2eml$3a20$2c14$2d$2d48$5d_409_closure@GOTPCREL(%rip), %rax
        call    camlCamlinternalFormat__make_printf_4967@PLT
.L129:
        movq    camlExample__full_apply_240@GOTPCREL(%rip), %rdi
        movq    %rax, %rsi
        movq    %rsp, %rbp
        movq    56(%r14), %rsp
        call    caml_initialize@PLT
        movq    %rbp, %rsp
        movq    camlExample__full_apply_240@GOTPCREL(%rip), %rax
        movq    (%rax), %rbx
        movq    camlExample__x_75@GOTPCREL(%rip), %rax
        movq    (%rax), %rax
        movq    (%rbx), %rdi
        call    *%rdi
.L130:
        movl    $1, %eax
        addq    $8, %rsp
        ret
.L122:
        push    $34
        call    caml_call_realloc_stack@PLT
        popq    %r10
        jmp     .L123

The Bad

Lambda problem

In general, the Rust compiler's error messages are quite helpful. This is important, because dealing (fighting) with the borrow checker is a frequence occurrence. Unfortunately, there are some cases that, despite a lot of effort, I still don't really understand.

Here is a problem that I posted on stack overflow. It's a bit contrived, but it happened because I had a very functional solution to part 1 of an Advent of Code problem. The easiest way to solve the second part was to add a mutation.

Here is the program:

fn main(){
  let v1=vec![1];
  let v2=vec![3];
  let mut v3=vec![];
  v1.iter().map(|x|{
    v2.iter().map(|y|{
      v3.push(*y);
    })
  });
}

And here is the error:

error: captured variable cannot escape `FnMut` closure body
 --> src/main.rs:6:5
  |
4 |     let mut v3=vec![];
  |         ------ variable defined here
5 |     v1.iter().map(|x|{
  |                     - inferred to be a `FnMut` closure
6 | /     v2.iter().map(|y|{
7 | |       v3.push(*y);
  | |       -- variable captured here
8 | |     })
  | |______^ returns a reference to a captured variable which escapes the closure body

The suggestions I received on stack overflow were basically "use loops". This was very disappointing for an example where the closures' scopes are clearly limited.

Anyway, it's still early days for Rust, so I hope that problems like this will be improved over time. Overall, it seems like a great language for doing systems development, but I still think a garbage collected language is better for daily driving.

One of the aspects I like about my job as a researcher at SEI is that I split my time between being an academic researcher and a software engineer. For example, a few years ago, my colleagues and I published a paper on how to employ logic programming to recover object-oriented abstractions from an executable. I was very proud of that paper (and still am!) because it introduces some interesting new approaches to performing binary analysis, and yet is also a usable tool (OOAnalyzer) that people are actually using to reverse engineer real software.

Although basing our system on logic programming made for an interesting paper, it also made it challenging to scale OOAnalyzer to very large and complex executables. We strugged from the beginning to achieve reasonable performance, and eventually concluded that we had to aggressively use tabling in order to achieve reasonable performance. At a high level, tabling is memoization for Prolog. Prolog does have side-effects, though, and part of the challenge for tabling implementations is to make sure that the tables are consistent.

One of the leading Prolog implementations with tabling support is XSB Prolog, which OOAnalyzer has been using since the beginning. Teri Swift, one of the XSB developers, and the leading expert on Prolog tabling, really helped us get enough performance to be able to write our paper. We were able to analyze some large and interesting programs, including mysql.exe, the MySQL client program. The largest program we were able to test in our paper was over 5 MiB.

Unfortunately, there were many programs that we weren't able to test successfully as well. One of these that really stuck in my mind was mysqld.exe. In our paper, we were able to run successfully on mysql.exe, the MySQL client program, but mysqld.exe, the daemon was much larger (22 MiB vs 5 MiB), and remained elusive.

A while after we published our paper, we started working again with Teri Swift, who was helping Jan Wielemaker of SWI Prolog add support for tabling to SWI Prolog. Teri and Jan wanted to use OOAnalyzer as a test case to make sure that SWI Prolog's tabling implementation was working correctly. Since this would mean that OOAnalyzer would have another supported Prolog engine, this was a win-win situation for us! Jan graciously helped us get OOAnalyzer running on SWI, which was useful in its own right. He also developed some invaluable debugging tools to help us understand what tabling is doing behind the scenes.

These tools, combined with a lot of profiling and rewriting iterations, eventually allowed us to improve performance bottlenecks to the point that we could successfully reason through mysqld.exe and other similarly large programs! Along the way, we battled performance bottlenecks, memory that would not be reclaimed, and other problems. But now we can analyze mysqld.exe in about 18 hours, and only using about 12 GiB of memory. And what is encouraging is that even near the end of reasoning about such a large program, the tool is still making new inferences fairly quickly.

These updates are available in the latest release of the Pharos repository. My colleague Cory Cohen recently wrote a tutorial on how to run OOAnalyzer on large executables, with all of the tricks we have learned over the years.

While working with Teri and Jan, I very slowly began to understand some of the underlying problems that would cause performance to degrade in large programs. One of the problems was that, to maintain consistency, the tabling implementation would re-compute tables from scratch. For most tables, this could be done quickly. But for others, it would take up huge amounts of time. I also realized that because of the structure of our problem, which incrementally learns new conclusions over time, the recomputations were not really needed.

I created a work-around in Prolog that I call "trigger rules". I rewrote the most expensive OOAnalyzer rules to be triggered when dependent facts were introduced, which avoided the costly (and unnecessary) recomputation of the table for all values. The conversion process is fragile and manual, but it proved that if we could avoid the costly recomputations, OOAnalyzer's performance would scale pretty well.

More recently, we've been working with Jan on some a tabling method that avoids the costly recomputations (and also avoids the fragile, error-prone manual transformations that I needed to make for trigger rules). The new type of tabling is called monotonic tabling. There are still some kinks to work out, but we are optimistic that this will further improve the performance of OOAnalyzer and make it easier to maintain.

And of course, monotonic tabling will probably make for an interesting subject of a new paper. So we've now come full circle. We wrote the research paper on OOAnalyzer. This led us to engineering challenges. And to solve the engineering challenges, it brought us back to a new research problem.